![[a[0], a[1], a[2], a[3], a[4], a[5], a[6], a[7], a[8], a[9], a[10], a[11], a[12], a[13], a[14], a[15], a[16], a[17], a[18], a[19], a[20]]](legendre_images/math0.png){kind=small}
Generador de Polinomios de Legendre
Este pequeño programa calcula los polinomios de Legendre por el método de Frobenius.
Debe elegir la variable grado, que debe ser el punto de truncamiento de la Serie de Taylor y
GradoMax el orden de la ecuación de Legendre,para un buen resultado GradoMax+2<=grado
grado:=20:GradoMax:=18:
assume(n in Z_)
assumeAlso(n>0)
a:=array(0..grado):
eqcoef:=array(0..grado):
Legendre:=array(1..GradoMax):
Incog:=[a[i] $ i = 0..grado];
y:=sum(a[n]*x^n,n=0..grado):
for GradoPol from 1 to GradoMax do
eq:=diff((1-x^2)*diff(y,x),x)+GradoPol*(GradoPol+1)*y:
if mods(GradoPol,2)=0 then
eqcoef[0]:=a[1]=0
else
eqcoef[0]:=a[0]=0
end_if:
eqcoef[1]:=a[GradoPol]=(2*GradoPol)!/(2^GradoPol*(GradoPol!)^2):
for i from 2 to grado do
eqcoef[i]:=coeff(eq,x,i-2)=0:
end_for:
Ecuaciones:=coerce(eqcoef,DOM_LIST):
Var:=solve(Ecuaciones,Incog):
Legendre[GradoPol]:=subs(y,op(Var,1)):
end_for
Legendre
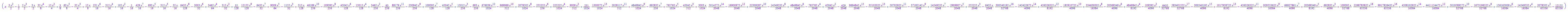
plot(Legendre[k] $ k=1..GradoMax,x=-1..1)
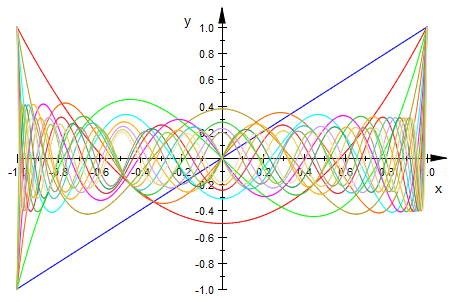
eqcoef
![array(0..20, (0) = a[1] = 0, (1) = a[18] = 2268783825/65536, (2) = 342*a[0] + 2*a[2] = 0, (3) = 340*a[1] + 6*a[3] = 0, (4) = 336*a[2] + 12*a[4] = 0, (5) = 330*a[3] + 20*a[5] = 0, (6) = 322*a[4] + 30*a[6] = 0, (7) = 312*a[5] + 42*a[7] = 0, (8) = 300*a[6] + 56*a[8] = 0, (9) = 286*a[7] + 72*a[9] = 0, (10) = 270*a[8] + 90*a[10] = 0, (11) = 252*a[9] + 110*a[11] = 0, (12) = 232*a[10] + 132*a[12] = 0, (13) = 210*a[11] + 156*a[13] = 0, (14) = 186*a[12] + 182*a[14] = 0, (15) = 160*a[13] + 210*a[15] = 0, (16) = 132*a[14] + 240*a[16] = 0, (17) = 102*a[15] + 272*a[17] = 0, (18) = 70*a[16] + 306*a[18] = 0, (19) = 36*a[17] + 342*a[19] = 0, (20) = 380*a[20] = 0)](legendre_images/math3.png)
int(Legendre[1]*Legendre[1]*sqrt(1-x^2),x=-1..1)
